Question

You bought 12 raffle tickets that are good for 4 raffles. If 715 total tickets were sold what is the probability that you will win at least 1 of the raffles?

Answer 1

0.06546.

Explanation:

Total number of tickets = 715

Good raffle tickets (Prize) = 4

Number of tickets bought = 12

`\text{Probability of winning}=\frac{\text{Number of tickets bought}}{\text{Total raffle tickets}}`

`\text{Probability of winning}=(12)/(715)`

`\text{Probability of not winning}=1-(12)/(715)=(703)/(715)`

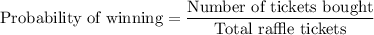
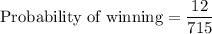
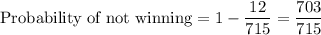
Let x be event of the number of winning prizes.

Probability that you will win at least 1 of the raffles is

`P(x\geq 1)=1-P(x=0)`

`P(x\geq 1)=1-^(4)C_0\left((12)/(715)\right)^0\left((703)/(715)\right)^(4-0)`

`P(x\geq 1)=1-\left((703)/(715)\right)^(4)`

`P(x\geq 1)=1-0.93454`

`P(x\geq 1)=0.06546`

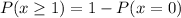
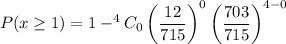
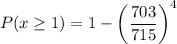
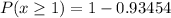
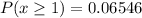
Therefore, the required probability is 0.06546.