Question

A bag of marbles contains 3 red marbles, 7 blue marbles, and 5 orange marbles. If a marble is drawn from the bag and not replaced, then a second marble is drawn. Calculate P(red then orange):

Answer 1

`(1)/(14)`.

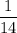Explanation:

It is given that,

Red marbles = 3

Blue marbles = 7

Orange marbles = 5

Total marbles = 3+7+5 = 15

Probability of getting a red marble is

`P(Red)=\frac{\text{Red marbles}}{\text{Total marbles}}`

`P(Red)=(3)/(15)`

`P(Red)=(1)/(5)`

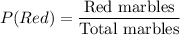
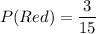
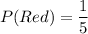
If a marble is drawn from the bag and not replaced. So remaining marbles is 15-1=14. Now,

Probability of getting an orange marble is

`P(orange )=\frac{\text{Orange  marbles}}{\text{Total remaining marbles}}`

`P(orange)=(5)/(14)`

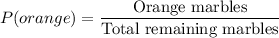
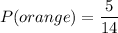
Now,

`P(\text{red then orange})=P(Red)* P(orange)`

`P(\text{red then orange})=(1)/(5)* (5)/(14)`

`P(\text{red then orange})=(1)/(14)`

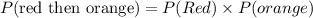
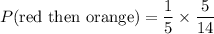
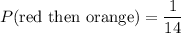
Therefore, the required probability is
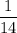`(1)/(14)`.