Question

Many states assess the skills of their students in various grades. One program that is available for this purpose is the National Assessment of Educational Progress (NAEP). One of the tests provided by the NAEP assesses the reading skills of twelfth-grade students. In a recent year, the national mean score was 289 and the standard deviation was 37. Assume that these scores are approximately Normally distributed, N(289, 37). How high a score is needed to be in the top 25% of students who take this exam (use technology)?

Answer 1

A score of 314 is needed to be in the top 25% of students who take this exam.

Explanation:

We are given that one of the tests provided by the NAEP assesses the reading skills of twelfth-grade students. In recent years, the national mean score was 289 and the standard deviation was 37.

Let X = scores of the tests provided by the NAEP

The z-score probability distribution for the normal distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = national mean score = 289

`\sigma` = standard deviation = 37

Now, we have to find how high a score is needed to be in the top 25% of students who take this exam, that means;

P(X > x) = 0.25 {where x is the required score}

P(
`(X-\mu)/(\sigma)` >
`(x-289)/(37)` ) = 0.25

P(Z >
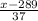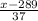`(x-289)/(37)` ) = 0.25

In the z table, the critial value of z that represents the top 25% of the area is given as 0.6745, that is;

`(x-289)/(37)=0.6745`

`{x-289}=0.6745* 37`

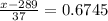
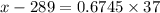
x = 289 + 24.96 = 313.96 ≈ 314

Hence, a score of 314 is needed to be in the top 25% of students who take this exam.