How do I solve this problem?

Question

asked Jul 24, 2021 28.1k views

1 Answer

Phann · Answer 1 · 2021-07-29T09:48:44+0000

Answer:

Explanation:

The first 2 pieces of this function agree at pi/4, so we will set them equal to each other and sub in pi/4 for x to solve for k:

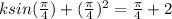$ksin((\pi)/(4))+((\pi)/(4))^2=(\pi)/(4)+2$ and

$k((√(2) )/(2))+(\pi^2)/(16)=(\pi)/(4)+2$ and we'll multiply everything by 16 to get rid of the fractions. Doing that gives us:

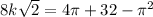$8k√(2)=4\pi+32-\pi^2$ and

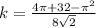$k=(4\pi+32-\pi^2)/(8√(2) )$ so

k = 3.067

The next one is a bit tricky if you're not up on your natural log equations.

Again, we set these equal to each other because they meet at the value of e. We sub in e for x and solve for m:

x +2=mlne^x

We'll sub in e for x. ln of e to the x power is equal to x, so

e + 2 = me and

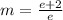m=(e+2)/(e) so

m = 1.736

Hope that helps!