Question

PLEASE HELP WITH PART 2! :)

Answer 1

• The equation is a contradiction

• The solution set is Ø

Explanation:

The simplest approach to this problem is solving for the value of y, and then identifying what type of equation it is. Remember that conditional equations have a defined value, contradiction equations have no solutions, and identity type equations have infinite solutions. Let's solve for y,

`\mathrm{Given:5y\:+\:5\:-\:11y\:=\:-\:2y\:-\:7\:-\:4y},\\\\\mathrm{Add\:similar\:elements:}\\\\=> -6y+5=-2y-7-4y\\=> -6y+6y=-6y-12+6y\\=>0=-12`

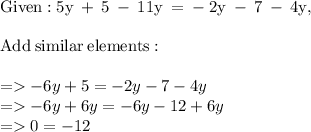
Both sides are not equal, and hence we have no solutions. Our equation is contradiction, and the solution set is Ø.

Answer 2

Steps to solve:

~Combine like terms

-6y + 5 = -6y - 7

~Subtract 5 to both sides

-6y = -6y - 12

~Add 6 to both sides

0 = -12

There are no solutions.

Best of Luck!