Answer:
(a) The linear depreciation function of the car which gives the worth of the car y after a number of years, t is given as follows;
y = 25,425 - 2,739 × t
(b) The value of the car 7 years from now is $6,252
(c) $2,739 per year
Explanation:
The manufacture's suggested retail price (MSRP) for the car = $25,425
The amount the car is expected to be worth in 5 years = $11,730
(a) The linear depreciation is given as follows;

Where;
Cost of Asset = $25,425
Salvage Value = $11,730
Life of Asset in use = 5 years
We get;
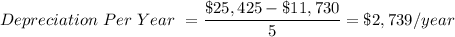
Therefore, the linear depreciation function, can be written as follows;
y - 25,425 = -2,739×(t - 0)
y = -2,739·t + 0 + 25,425 = 25,425 -2,739·t
y = 25,425 - 2,739 × t
Where;
y = The expected worth of the car after a given number of years
t = The number of years used for the calculation of the depreciation
(b) The value of the car 7 years from now is given by substitution as follows;
Whet t = 7, we have;
y = 25,425 -2,739·t = y = 25,425 -2,739 × 7 = $6,252
The value of the car 7 years from now = $6,252
(c)
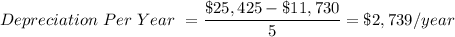
The car is depreciating at a rate of $2,739 per year.