Answer:
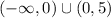 .
.
Explanation:
Note: In the given options it should be negative infinity instead of -0 because -0 does not make any sense.
It is given that cube of a number is less than five times the square of the number.
Let the unknown number be x.

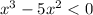
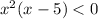
This is possible when both factors
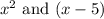 have different sign.
have different sign.
We know that
 is always greater than or equal to 0. So,
is always greater than or equal to 0. So,
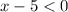
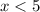
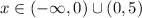
Because
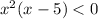 is not true for x=0, so, 0 is not included in the solution set.
is not true for x=0, so, 0 is not included in the solution set.
Therefore, the solution set is
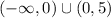 .
.