Question

Use the difference quotient to calculate the average rate of change across the following intervals. Difference quotient of d(t): 3t^2 + 5th – 2

The interval 2 to 3:

The interval 2 to 2.5:

The interval 2 to 2.1:

Answer 1

2 to 3 is 20

2 to 2.5 is 15

2 to 2.1 is 11

Explanation:

I got this question right on EDGE 2023

Answer 2

Ok, we have:

d(t) = 3*t^2 + 5*t - 2.

The first interval is:

(2, 3)

and remember that, for an interval (a,b), the difference quotient is:

D = (f(b) - f(a))/(b -a)

Then in this first interval we have:

`d = (d(3) - d(2))/(3-2) = (3*3^2 + 5*3 - 2 - (3*2^2 + 5*2 - 2))/(1) = 20`

So the average rate of change in (2,3) is 20.

now, in (2, 2.5) we have:

`d = (d(2.5) - d(2))/(3-2) = (3*2.5^2 + 5*2.5 - 2 - (3*2^2 + 5*2 - 2))/(1) = 9.25`

So here the rate of change is 9.25

And in the interval (2, 2.1) we have:

`d = (d(2.1) - d(2))/(3-2) = (3*2.1^2 + 5*2.1 - 2 - (3*2^2 + 5*2 - 2))/(1) = 1.73`

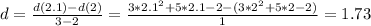
So in this interval the rate of change is 1.73