Question

Gwen releases a rock at rest from the top of a 40-m tower. If g = 9.8 m/s2 and air resistance is negligible, what is the speed of the rock as it hits the ground?

Answer 1

Using the kinematic equation for constant acceleration, we determine that the speed of the rock as it hits the ground is 28 m/s.

Step-by-step explanation:

To determine the speed of the rock as it hits the ground, we can use the kinematic equation for constant acceleration:

v^2 = u^2 + 2as

Where:

• v is the final velocity,
• u is the initial velocity (which is 0 since the rock is released from rest),
• a is the acceleration due to gravity (9.8 m/s2), and
• s is the distance fallen (40 m).

Since the initial velocity u is 0, the equation simplifies to:

v^2 = 2as

Substituting the values of a (9.8 m/s2) and s (40 m), we calculate:

v^2 = 2 × 9.8 m/s2 × 40 m

v^2 = 784 m2/s2

Therefore, the final velocity v is:

v = √784 m2/s2 = 28 m/s

The rock hits the ground with a speed of 28 m/s.

Answer 2

`28\; \rm m \cdot s^(-1)`.

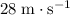Step-by-step explanation:

Short Explanation

Apply the SUVAT equation
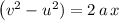`\left(v^2 - u^2) = 2\, a \, x`, where:

• 
  `v` is the final velocity of the object,
• 
  `u` is the initial velocity of the object,
• 
  `a` is the acceleration (should be constant,) and
• 
  `x` is the displacement of the object while its velocity changed from
  `v` to
  `u`.

Assume that going downwards corresponds to a positive displacement. For this question:

• 
  `v` needs to be found.
• 
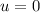  `u = 0` because the rock is released from rest.
• 
  `a = g = 9.8 \; \rm m\cdot s^(-2)`.
• 
  `x = 40\; \rm m`.

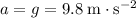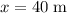Solve this equation for
`v`:

`\displaystyle v = √(2\, a\, x + u^2) = √(2* 9.8 * 40) = 28\; \rm m \cdot s^(-1)`.

In other words, the rock reached a velocity of
`28\; \rm m\cdot s^(-1)` (downwards) right before it hits the ground.

Explanation

Let
`v` be the velocity (in
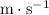`\rm m \cdot s^(-1)`) of this rock right before it hits the ground. Under the assumptions of this question, it would take a time of
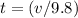`t = (v / 9.8)` seconds for this rock to reach that velocity if it started from rest and accelerated at
`9.8\; \rm m \cdot s^(-2)`.

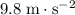Note that under these assumptions, the acceleration of this rock is constant. Therefore, the average velocity of this rock would be exactly one-half the sum of the initial and final velocity. In other words, if
`u` denotes the initial velocity of this rock, the average velocity of this rock during the fall would be:

`\displaystyle (u + v)/(2)`.

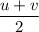On the other hand,
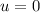`u = 0` because this stone is released from rest. Therefore, the average velocity of this rock during the fall would be exactly
`(v / 2)`.

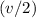The displacement of an object over a period of time is equal to the length of that period times the average velocity over that period. For this rock, the length of this fall would be
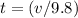`t = (v / 9.8)`, while the average velocity over that period would be
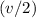`(v / 2)`. Therefore, the displacement (in meters) of the rock during the entire fall would be:

`\displaystyle \left((v)/(2)\right) \cdot \left((v)/(9.8)\right) = (v^2)/(19.6)`.

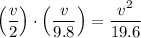That displacement should be equal to the change in the height of the rock,
`40\; \rm m`:

`\displaystyle (v^2)/(19.6) = 40`.

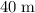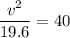Solve for
`v`:

`v = 28\; \rm m \cdot s^(-1)`.

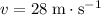Once again, the speed of the rock would be
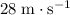`28\;\rm m \cdot s^(-1)` right before it hits the ground.