Answer:
C
Explanation:
To do this, let's let the decimal equal n. Thus:
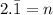
There is only one digit repeating, so let's multiply both sides of the equation by 10:
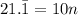
Now, subtract n from both sides:
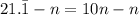
On the right, it becomes 9n. However, the left, however, expand, the decimal. In other words:
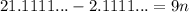
All of the repeating 1s will cancel out. Thus:
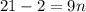
Subtract:
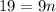
Divide both sides by 9:
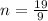
And since we set the decimal equal to n originally...
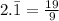
And we're done!
Notes:
This is the algebraic way to write a repeating decimal into a fraction. You can, of course, always just use a calculator and guess and check.