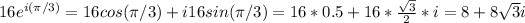Question

6


math geniuses help please!!


math

Answer 1

A

Explanation:

Begin with Euler's formula. I am assuming youre aware of this if youre taking complex algebra? You can prove Euler's formula by doing a Maclaurin expansion of cosine, sine, and e^x. Euler's formula states that:

`e^(ix)=cos(x)+isin(x)`

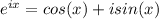
We can put the first complex number in exponetial form by noticing the input is 2pi/3. The second complex number has an input of pi/3. Therefore:

`z_1=8e^(i(2\pi /3))`

`z_2=0.5e^(i(\pi /3))`

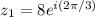
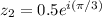
Then:

`(z_1)/(z_2) =(8e^(i(2\pi /3)))/(0.5e^(i(\pi /3)))`

Simplify the coefficients to get:

`(z_1)/(z_2) =(16e^(i(2\pi /3)))/(e^(i(\pi /3)))`

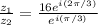
When you divide exponentials, you subtract the exponents. Therefore:

`(z_1)/(z_2) =16e^(i(2\pi /3)-i(\pi /3))=16e^{i(\pi /3)`

Put it back into trigonemtric form using Euler's formula:

`16e^(i(\pi /3))=16cos(\pi /3)+i16sin(\pi /3)`

Cosine of pi/3 is 0.5, and sine of pi/3 is square root of 3 over 2. We have:

`16e^(i(\pi /3))=16cos(\pi /3)+i16sin(\pi /3)=16*0.5+16*(√(3) )/(2) *i=8+8√(3) i`