Question

Please assist me with these problems and show the work. Part 1 4. From a horizontal distance of 80.0 m, the angle of elevation to the top of a fragpole is 18°. Calculate the height of the flagpole to the nearest tenth of a metre. 5. A 9.0 m ladder rests against the side of a wall. The bottom of the ladder is 1.5 m from the base of the wall. Determine the measure of the angle between the ladder and the ground, to the nearest degree.

Answer 1

4) About 26.0 feet

5) About 80 degrees.

Explanation:

Answer 2

4) About 26.0 feet

5) About 80 degrees.

Explanation:

Please refer to the (badly drawn, sorry) drawings.

4)

So for a horizontal distance of 80 meters, the angle of elevation is 18 degrees. And we want to find the height.

The horizontal distance is adjacent to the angle, and the height is opposite to the angle. Thus, we can use the trigonometric ratio tangent.

Recall that tangent is:

`\tan(x)=opp/adj`

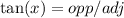
Substitute 18 for x, h for opposite, and 80 for adjacent. Thus:

`\tan(18)=(h)/(80)`

To solve for h, multiply both sides by 80:

`h=80\tan(18)`

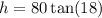
Use a calculator:

`h\approx25.9938`

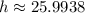
So, the height is approximately 26.0 feet.

5)

So, this time, we need to find the angle. We know the hypotenuse and the side adjacent to the angle. So, we can use cosine. Recall that:

`\cos(x)=adj/hyp`

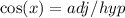
Substitute 1.5 for adjacent and 9 for the hypotenuse. Thus:

`\cos(x)=(1.5)/(9)`

Take the inverse cosine of both sides:

`x=\cos^(-1)((1.5)/(9))`

Use a calculator:

`x\approx80.4059\textdegree\approx80\textdegree`

So, the angle is about 80 degrees.

And we're done!