Question

Find the midpoint of a and b where a has the coordinates (8,5) and b has.coordinates (3,7)

Answer 1

We've been given to find out the midpoint coordinates in which the two coordinates has points (8,5) and (3,7).

The standard formula for calculating midpoint of two given coordinates are,

`\implies\sf{( (x_1 + x_2)/(2) )( (y_1 + y_2)/(2) )}`

Here we have following data:

• x1 =8 and y1= 5

• x2 = 3 and y2 = 7

Replacing the values in formula we get,

`\implies\sf{( (8 + 3)/(2) ) , ( (5 + 7)/(2)) }`

`\implies\sf{( (11)/(2) ) , ( (12)/(2) )}`

`\implies\sf{(5.5) , (6)}`

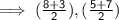
• The coordinates of midpoint are (5.5,6)

Answer 2

(5.5 , 6)

Explanation:

`Midpoint \left((x_(1)+x_(2))/(2),(y_(1)+y_(2))/(2)\right)\\\\\\\left((8+3)/(2),(5+7)/(2) \right)\\\\\\=\left((11)/(2),(12)/(2)\right)\\\\\\=\left(5.5,6 \right)`