Question

How do you find the area?

Answer 1

• First attachment's graph is correct

• Second attachment, the area is approximately 8.6

Explanation:

Remember that the area between two curves is defined as the following:

`\mathrm{The\:area\:between\:curves\:is\:the\:area\:between\:curve\:f(x)\:and\:curve\:g(x)\:on\:interval\:[a,b]} :\\A=\int _a^b|f\left(x\right)-g\left(x\right)|dx`

We are given the curves y = 7cos(2x), and y = 7 - 7cos(2x) on interval [0, π/2]. Therefore, applying the area formula, we have the solve the following integral:

`\int _0^{(\pi )/(2)}\left|7\cos \left(2x\right)-\left(7-7\cos \left(2x\right)\right)\right|dx`

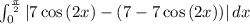
From now on take a look at the attachment. It shows how to solve the integral, and it's exact value. The area is not 9.727 as you entered, it is approximately 8.6. Your graph however was accurate, but there can be no work shown for that as it's much easier to use a graphing calculator.