Question

Hi.

i need help with this question.

Workings Please.

1. A 210° sector of a circle of radius 10cm is used to make a cone. Find the radius of the base of the cone and it's height.​

Answer 1

Answer: radius = 5.83 cm height = 8.12 cm

Explanation:

First, let's find the circumference of the 210° section of the circle.

`C=2\pi r\bigg((\theta)/(360^o)\bigg)\\\\\\C=2\pi(10)\bigg((210^o)/(360^o)\bigg)\\\\\\C=(35)/(3)\pi`

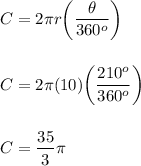
The circumference of the the cone is
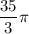`(35)/(3)\pi` . We can use this to find the radius .

`C=2\pi r\\\\(35)/(3)\pi=2\pi r\\\\\\(35\pi)/(3\cdot 2\pi)=r\\\\\\(35)/(6)=r\\\\\\5.83=r`

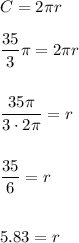
When you fold the 210° section into a cone, the slant height is the original radius of 10. We can use the radius and slant height of the cone to form a right triangle with the height. Use the Pythagorean Theorem to find the height.

radius² + height² = slant height²

`(35)/(6)^2\ +\ h^2=10^2\\\\\\.\qquad \quad h^2=10^2-\bigg((35)/(6)\bigg)^2\\\\.\qquad \quad h=\sqrt{(6^2(10)^2-35^2)/(6^2)}\\\\\\.\qquad \quad h=\sqrt{(2375)/(36)}\\\\\\.\qquad \quad h=8.12`