We've been given to find out the midpoint coordinates in which the two coordinates has points (8,5) and (3,7).
The standard formula for calculating midpoint of two given coordinates are,
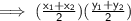
Here we have following data:
Replacing the values in formula we get,
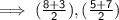
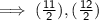
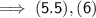
- The coordinates of midpoint are (5.5,6)