Question

4∣3c+5∣=16c I know the answer is five but I don't know how to get there

Answer 1

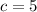`c = 5`, explanation for how to get there

Explanation:

If we have the equation
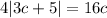`4|3c+5| = 16c`, we want to isolate c on one side and find it's value.

Let's first divide both sides by 4.

`4|3c+5|/4 = 16c/4\\\\|3c + 5| = 4c`

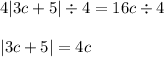
Now let's solve for the absolute value. We know that:

`3c + 5 = 4c`

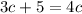
or

`3c + 5 = -4c`

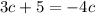
Possibility 1:

`3c + 5 = 4c`

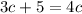
Subtract 3c from both sides:

`5 = c`

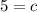
Possibility 2:

`3c + 5 = -4c`

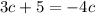
Add 4c to both sides:

`7c + 5 = 0`

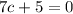
Subtract 5 from both sides:

`7c = -5`

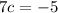
Divide both sides by 7:

`c = (-5)/(7)`

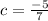
Plugging both of these values into the equation, we can see that only 5 works.

Hope this helped!