Answer:
When the gravitational force on the Moon from the Earth = 4.00 Fm, the distance of the Moon from the Earth is 0.5·D
Step-by-step explanation:
The given information includes;
The distance of the moon from the Earth = 0.25·D
The gravitational force, F, on the Moon from the Earth = 16.00 Fm
When the gravitational force on the Moon from the Earth = 4.00 Fm, the distance of the Moon from the Earth is found as follows;
From Newton's law of gravitation;
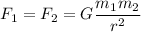
At r = 0.25·D, F = 16.00 Fm
Therefore;
G×m₁×m₂ = (0.25·D)²×16.00 Fm = D²×Fm = Constant
When, the gravitational force of the Moon from the Earth = 4.00 Fm, we have;

Therefore;
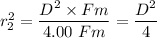
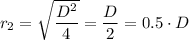
r₂ = 0.5·D
Where;
r₂ = The new distance of the Moon from the Earth
Therefore the distance of the Moon from the Earth when the gravitational force on the Moon from the Earth = 4.00 Fm is r₂ = 0.5·D.