Question

If M is the midpoint of XY, XM=2x+5 and YM=25, find XY.

Answer 1

50?

X_________M__________Y

2x + 5 = 25

x = 10 so 2(10) + 5 = 25

25 + 25 = 50

Answer 2

50

Explanation:

Since M is the midpoint of XY, this means that XM and MY must be equivalent from the definition of midpoint.

So:

`XM=MY`

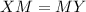
The entire length of the segment (XY) is:

`XY=XM+MY`

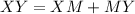
We know that XM is equivalent to MY. Substitute MY for XM:

`XY=MY+MY`

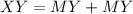
Combine like terms;

`XY=2MY`

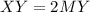
We are told that YM (or MY) is 25. So:

`XY=2(25)`

Multiply:

`XY=50`

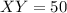
So, the length of XY is 50.

And we're done!