Question

What is the 8th term of this geometric sequence?
1, 3, 9, 27,...

Answer 1

1*3*3*3*3*3*3=729. For each term you multiply the previous term by three.

Answer 2

2187

Explanation:

To find the 8th term, we can find and use the explicit formula.

The standard form of the explicit formula for a geometric sequence is:

`x_n=a(r)^(n-1)`

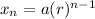
Where a is the initial term, r is the common ratio, and n is the nth term.

From the sequence, we can see that the first term is 1, and each term is 3 times the previous term. Thus, the common ratio is 3.

Substituting these into our equation, we will have:

`x_n=1(3)^(n-1)\\x_n=(3)^(n-1)`

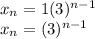
So, to find the 8th term, substitute 8 for n:

`x_8=(3)^(8-1)`

Subtract:

`x_8=(3)^7`

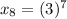
Evaluate:

`x_8=2187`

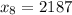
So, the 8th term is 2187.

And we're done!