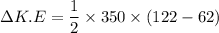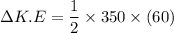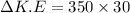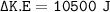Answer:
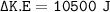
Explanation:
Given that:
the expression for the change in kinetic energy =
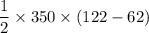
Recall that
Kinetic energy K.E =
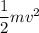
where,
m = mass of the horse
v = velocity of the horse
The change in kinetic energy between two instant times can be expressed by the relation
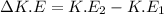
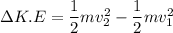
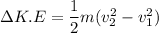
where;
m = 350
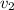 = 122
= 122
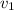 = 62
= 62