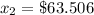Question

Customers at a certain pharmacy spend an average of $54.40, with a standard deviation of $13.50.What are the largest and smallest amounts spent by the middle 50% of these customers?

Answer 1

Largest is
`x_2 = \$ 63.506`

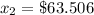
Smallest is
`x_1 = \$ 45.29`

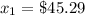
Explanation:

From the question we are told that

The mean is
`\mu = \$ 54.40`

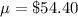
The standard deviation is
`\sigma = \$ 13.50`

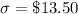
The largest and the smallest amount spent by 50% of the costumer is mathematically represented as

`P(x_1 < X < x_2) = P(( x_1 -\mu)/(\sigma ) < (X - \mu )/( \sigma ) < ( x_2 -\mu)/(\sigma ) ) = 0.50`

=>
`P(x_1 < X < x_2 ) = P((x_1 - 54.40)/( 13.50) < X < (x_2 - 54.40)/( 13.50) ) = 0.50`

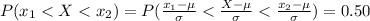
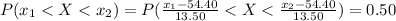
Given that this is normally distributed we have that

`P(X <- (x_1 - 54.40)/( 13.50) ) = 0.25`

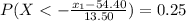
and

`P(X < (x_2 - 54.40)/( 13.50) ) = 0.25`

From the normal distribution curve that z-score having a probability of 0.25 is

0.6745

So

`(x_1 - 54.40)/( 13.50) = -0.6745`

=>
`x_1 = \$ 45.29`

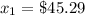
and

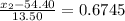
`(x_2 - 54.40)/( 13.50) = 0.6745`

=>
`x_2 = \$ 63.506`