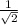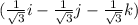Question:
Express each vector as a product of its length and direction.
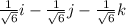
Answer:
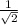
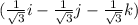
Explanation:
A vector v can be expressed as a product of its length and direction as follows;
v = |v| u
Where;
|v| = length/magnitude of v
u = unit vector in the direction of v
---------------------------------------------------------------------------------------
Let the given vector be v, i.e
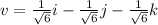
(i) The length/magnitude |v| of vector v is therefore,
|v| =
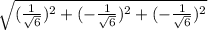
|v| =

|v| =

|v| =
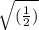
|v| =
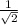
(ii) The unit vector u in the direction of vector v, is therefore,
u =
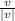
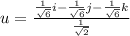
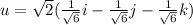
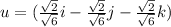
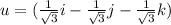
Therefore, the vector can be expressed as a product of its length and direction as:
|v| u =