Question

A glass plate 2.25 mm thick, with an index of refraction of 1.80, is placed between a point source of light with wavelength 620 nm (in vacuum) and a screen. The distance from source to screen is 1.50 cm. How many wavelengths are there between the source and the screen?

Answer 1

There are 2.71x10⁴ wavelengths between the source and the screen.

Step-by-step explanation:

The number of wavelengths (N) can be calculated as follows:

`N = (d_(g))/(\lambda_(g)) + (d_(a))/(\lambda_(a))`

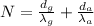
Where:

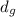`d_(g)`: is the distance in glass = 2.25 mm

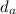`d_(a)`: is the distance in air = 1.50 cm - 0.225 cm = 1.275 cm

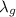`\lambda_(g)`: is the wavelength in glass

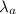`\lambda_(a)`: is the wavelength in air = 620 nm

To find the wavelength in glass we need to use the following equation:

`n_(g)*\lambda_(g) = n_(a)*\lambda_(a)`

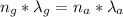
Where:

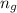`n_(g)`: is the refraction index of glass = 1.80

`n_(a)`: is the refraction index of air = 1

`\lambda_(g) = (\lambda_(a))/(n_(g)) = (620 nm)/(1.80) = 344.4 nm`

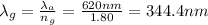
Hence, the number of wavelengths is:

`N = (d_(g))/(\lambda_(g)) + (d_(a))/(\lambda_(a))`

`N = (2.25 \cdot 10^(-3) m)/(344.4 \cdot 10^(-9) m) + (1.275 \cdot 10^(-2) m)/(620 \cdot 10^(-9) m)`

`N = 2.71 \cdot 10^(4)`

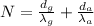
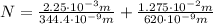
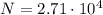
Therefore, there are 2.71x10⁴ wavelengths between the source and the screen.

I hope it helps you!