Question

The steady, surface temperature of a lake changes from point to point and is given to you as a function T(x, y) (assume the surface of the lake is in the (x,y) plane). If you attach a thermometer to a boat and take a path across the lake surface defined by the trajectory (x(t), y(t)) = (bi(t), b2(t)), find an expression for the rate of change of the thermometer temperature in terms of the lake temperature.

Answer 1

`(To - T)/(To - T_(infinity) ) = 1 - e^{(-bast)/(mc) }`

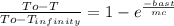
Explanation:

Attached below is the detailed expression

Given function : T(x,y)

assuming surface of the lake is in (x,y) plane

path across the lake surface = (x(t), y(t)) = ( bi(t), b2(t))

In other to find an expression we have to make some assumptions