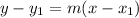Answer:
The equation of the tangent line

Explanation:
Step(i):-
Given function y = x cot (x) ....(i)
Differentiating equation (i) with respective to 'x' , we get
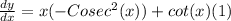
Step(ii):-
The slope of the tangent line
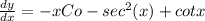
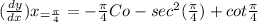
We will use trigonometry formulas

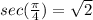
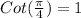
Now the slope of the tangent
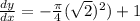
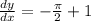
Step(iii):-
Given
Substitute
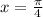 in y = x cot (x)
in y = x cot (x)

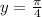
The point of the tangent line
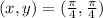
The equation of the tangent line