Question

After being treated with chemotherapy, the radius of the tumor decreased by 23%. What is the corresponding percentage decrease in the volume of the tumor

Answer 1

The volume of the tumor experimented a decrease of 54.34 percent.

Explanation:

Let suppose that tumor has an spherical geometry, whose volume (
`V`) is calculated by:

`V = (4\pi)/(3)\cdot R^(3)`

Where
`R` is the radius of the tumor.

The percentage decrease in the volume of the tumor (
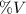`\%V`) is expressed by:

`\%V = (\Delta V)/(V_(o)) * 100\,\%`

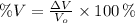
Where:

`\Delta V` - Absolute decrease in the volume of the tumor.

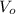`V_(o)` - Initial volume of the tumor.

The absolute decrease in the volume of the tumor is:

`\Delta V = V_(o)-V_(f)`

`\Delta V = (4\pi)/(3)\cdot (R_(f)^(3)-R_(o)^(3))`

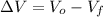
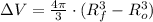
The percentage decrease is finally simplified:

`\%V = \left[1-\left((R_(f))/(R_(o))\right)^(3) \right]* 100\,\%`

Given that
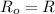`R_(o) = R` and
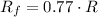`R_(f) = 0.77\cdot R`, the percentage decrease in the volume of tumor is:

`\%V = \left[1-\left((0.77\cdot R)/(R)\right)^(3) \right]* 100\,\%`

`\%V = 54.34\,\%`

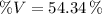
The volume of the tumor experimented a decrease of 54.34 percent.