Question

What should the ^14_6C content (in percent of y0) of a fossilized tree that is claimed to be 3000 years old?

Answer 1

The current mass fraction of
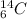`^(14)_(6) C` should be approximately 68.8 percent.

Step-by-step explanation:

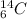`^(14)_(6) C` is a radioactive isotope with a halflife of 5568 years. The decay of any radioisotope is modelled after the following ordinary differential equation:

`(dm)/(dt) = -(m)/(\tau)`

Where:

`m` - Current mass of the isotope, measured in grams.

`\tau` - Time constant, measured in years.

The solution of this equation is of the form:

`m(t) = m_(o)\cdot e^{-(t)/(\tau) }`

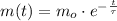
Where:

`t` - Time, measured in years.

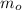`m_(o)` - Initial mass of the isotope, measured in grams.

The time constant can be found as a function of halflife (
`t_(1/2)`):

`\tau = (t_(1/2))/(\ln 2)`

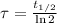
If
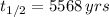`t_(1/2) = 5568\,yrs` and
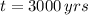`t = 3000\,yrs`, the mass fraction of
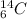`^(14)_(6) C` is:

`\tau = (5568\,yrs)/(\ln 2)`

`\tau \approx 8032.926\,yrs`

`(m(3000\,yrs))/(m_(o)) = e^{-(3000\,yrs)/(8032.926\,yrs) }`

`(m(3000\,yrs))/(m_(o)) \approx 0.688`

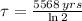
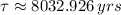
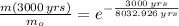
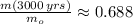
The current mass fraction of
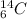`^(14)_(6) C` should be approximately 68.8 percent.