Answer:
599.7 m
approximately 600 m
Step-by-step explanation:
initial speed of the rocket = 0
net acceleration upwards = 7 m/s^2
the engine cuts out 10 sec after take off
maximum height reached = ?
we neglect air resistance
To get the velocity of the rocket at the point where the engine cuts off, we use the equation
v = u + at
where
v is the velocity at this point where the engine stops = ?
u is the initial velocity of the rocket from rest = 0 m/s
a is the net acceleration upwards = 7 m/s^2
t is the time the engine runs = 10 s
substituting, we have
v = 0 + (7 x 10)
v = 70 m/s
to get the distance from the ground to this point, we use the equation
 =
=
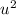 + 2as
+ 2as
where
v is the final velocity at the the height where the engine is cut out = 70 m/s
u is the initial speed at the ground = 0 m/s
a is the net acceleration on the rocket = 7 m/s^2
s is the distance from the ground to this point
substituting, we have
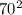 =
=
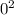 + 2(7 x s)
+ 2(7 x s)
4900 = 14s
s = 4900/14 = 350 m
After this point when the engine cuts out, the rocket experiences an acceleration proportional to the acceleration due to gravity 9.81 m/s^2 downwards, and slows down gradually before coming to a stop at the maximum height.
To get this height, we use the equation
 =
=
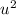 - 2gs (the negative sign is due to the downward direction of the acceleration g)
- 2gs (the negative sign is due to the downward direction of the acceleration g)
where
v is the final velocity at the maximum height = 0 m/s (it comes to a stop)
u is the speed at the instance that the engine is cut out = 70 m/s
g is the acceleration due to gravity = 9.81 m/s^2
s is the distance from this point to the maximum height
substituting values, we have
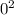 =
=
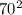 - 2(9.81 x s)
- 2(9.81 x s)
0 = 4900 - 19.62s
4900 = 19.62s
s = 4900/19.62 = 249.7 m
The maximum height that will be reached = 350 m + 249.7 m = 599.7 m
approximately 600 m