Answer:
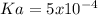
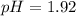
Step-by-step explanation:
Hello,
In this case, given the percent ionization and the concentration of the acid, one computes the concentration of hydrogen ions as follows:
![\% ionization=([H^+])/([HA])*100\%](https://img.qammunity.org/2021/formulas/chemistry/college/t8wtklcfl9s70wrzo999j9lr8jx4no99sj.png)
![[H^+]=(\% ionization*[HA])/(100\%) =(4\%*0.30M)/(100\%)=0.012M](https://img.qammunity.org/2021/formulas/chemistry/college/gl7pcfdf6c4mih4q3bmvcpm1kyzkqdpkwv.png)
Therefore the Ka is computed by using the equilibrium expression:
![Ka=([H^+][A^-])/([HA]) =(0.012M*0.012M)/(0.30M-0.012M)\\ \\Ka=5x10^(-4)](https://img.qammunity.org/2021/formulas/chemistry/college/uzju9dg5p9kc9rw3ystgkl3ou0zwq1rl08.png)
And the pH:
![pH=-log([H^+])=-log(0.012)\\\\pH=1.92](https://img.qammunity.org/2021/formulas/chemistry/college/j33q8jazs35xmhkifdmn46ihexbwuea52v.png)
Regards.