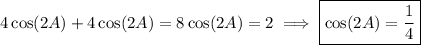Question

Hard question please help. I had to repost because last time I wanted to give more points but I forgot to.

If
`(\sin^2 3A)/(\sin^2 A) - (\cos^2 3A)/(\cos^2 A) = 2` find what
`\cos2A` is.

Best Answer gets the reaming 15!
Have Fun!

Answer 1

Use the angle sum identities to expand
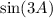`\sin(3A)` and
`\cos(3A)`:

`\sin(3A)=\sin(A+2A)=\sin A\cos(2A)+\cos A\sin(2A)`

`\cos(3A)=\cos(A+2A)=\cos A\cos(2A)-\sin A\sin(2A)`

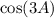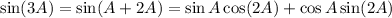
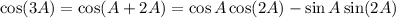
Use the double angle identity to expand
`\sin(2A)`:

`\sin(2A)=2\sin A\cos A`

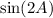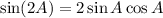
So we have

`\sin(3A)=\sin A\cos(2A)+2\cos^2A\sin A`

`\cos(3A)=\cos A\cos(2A)-2\sin^2A\cos A`

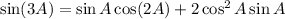
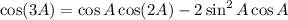
Then divide the first expression by
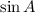`\sin A` and the second by
`\cos A`:

`(\sin(3A))/(\sin A)=\cos(2A)+2\cos^2A`

`(\cos(3A))/(\cos A)=\cos(2A)-2\sin^2A`

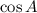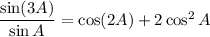
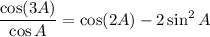
Squaring these gives

`(\sin^2(3A))/(\sin^2A)=(\cos(2A)+2\cos^2A)^2=\cos^2(2A)+4\cos(2A)\cos^2A+4\cos^4A`

`(\cos^2(3A))/(\cos^2A)=(\cos(2A)-2\sin^2A)^2=\cos^2(2A)-4\cos(2A)\sin^2A+4\sin^4A`

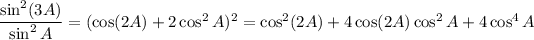
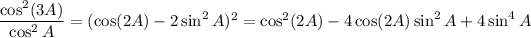
Subtract the second expression from the first to get the original equation. The
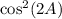`\cos^2(2A)` terms cancel, leaving us with

`4\cos(2A)\cos^2A+4\cos^4A+4\cos(2A)\sin^2A-4\sin^4A=2`

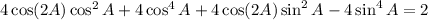
Now, notice that

`4\cos(2A)\cos^2A+4\cos(2A)\sin^2A=4\cos(2A)(\cos^2A+\sin^2A)=4\cos(2A)`

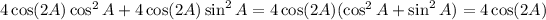
and

`4\cos^4A-4\sin^4A=4(\cos^2A-\sin^2A)(\cos^2A+\sin^2A)=4\cos(2A)`

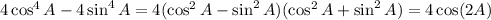
because
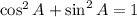`\cos^2A+\sin^2A=1` and
`\cos^2A-\sin^2A=\cos(2A)`.

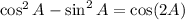So we're left with

`4\cos(2A)+4\cos(2A)=8\cos(2A)=2\implies\boxed{\cos(2A)=\frac14}`