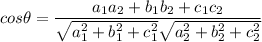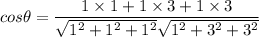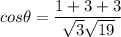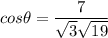Question

Consider the following planes. x + y + z = 5, x + 3y + 3z = 5A) Find parametric equations for the line of intersection of the planes. B) Find the angle between the planes.

Answer 1

Explanation:

Consider the following planes. x + y + z = 5, x + 3y + 3z = 5

the parametric equations for the line of intersection of the planes are determined as follows:

From the first plane, the normal of the first plane is
`n_1 = (1,1,1)`

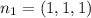
from the second plane, the normal of the second plane is
`n_2 = (1,3,3)`

`n_1 * n_2 = \begin {vmatrix} \left \begin{array}{ccc}i&j&k\\1&1&1\\1&3&3 \end{array}\right \end {vmatrix}`

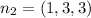
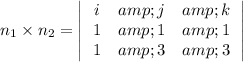
= i(3-3) -j(3-1)+k(3-1)

= i(0) - j(2) + k(2)

= -2j +2k

Suppose z = 0

x+y + 0 = 5 ---(1)

x+3y + 3(0) = 5 (2)

subtracting by elimination

-2y = 0

y = 0/-2

y = 0

The intersection on point of the plane is (5,0,0)

The equation of plane is r (t) =(5, 0, 0) + t(0, -2, 2)

∴

(x(t), y (t), z(t) ) = (5, -2t, 2t)

B) Find the angle between the planes

The angle between the planes can be represented by the equation:

`cos \theta = (a_1a_2+b_1b_2 + c_1c_2)/(√(a^2_1+b_1^2+c_1^2)√(a_2^2+b_2^2+c_2^2))`

`cos \theta = (1 * 1+1* 3 +1 * 3)/(√(1^2+1^2+1^2)√(1^2+3^2+3^2))`

`cos \theta = (1+ 3 +3)/(√(3)√(19))`

`cos \theta = (7)/(√(3)√(19))`

`\mathbf{\theta = cos ^(-1) ((7)/(√(57)))}`