Question

Solve the matrix equation for a, b, c, and d. [1 2] [a b] [6 5][3 4] [c d]= [19 8]

Answer 1

The answer is "
`\bold{\left[\begin{array}{cc}a&b\\c&d\end{array}\right] = \left[\begin{array}{cc}7&-2\\ -(1)/(2)&(7)/(2)\end{array}\right]}`".

Explanation:

`\bold{\left[\begin{array}{cc}1&2\\3&4\end{array}\right] \left[\begin{array}{cc}a&b\\c&d\end{array}\right] = \left[\begin{array}{cc}6&5\\ 19&8\end{array}\right]}`

Solve the L.H.S part:

`\left[\begin{array}{cc}1&2\\3&4\end{array}\right] \left[\begin{array}{cc}a&b\\c&d\end{array}\right]\\\\\\\left[\begin{array}{cc}a+2c&b+2d\\3a+4c&3b+4d\end{array}\right]`

After calculating the L.H.S part compare the value with R.H.S:

`\left[\begin{array}{cc}a+2c&b+2d\\3a+4c&3b+4d\end{array}\right]= \left[\begin{array}{cc}6&5\\ 19&8\end{array}\right]} \\\\`

`\to a+2c =6....(i)\\\\\to b+2d =5....(ii)\\\\\to 3a+4c =19....(iii)\\\\\to 3b+4d = 8 ....(iv)\\\\`

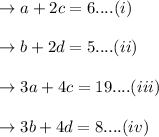
In equation (i) multiply by 3 and subtract by equation (iii):

`\to 3a+6c=18\\\to 3a+4c=19\\\\\text{subtract}... \\\\\to 2c = -1\\\\\to c= - (1)/(2)`

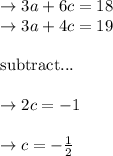
put the value of c in equation (i):

`\to a+ 2 (- (1)/(2))=6\\\\\to a- 2 * (1)/(2)=6\\\\\to a- 1=6\\\\\to a =6 +1\\\\\to a = 7\\`

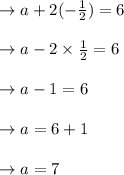
In equation (ii) multiply by 3 then subtract by equation (iv):

`\to 3b+6d=15\\\to 3b+4d=8\\\\\text{subtract...}\\\\\to 2d = 7\\\\\to d= (7)/(2)\\`

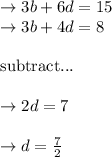
put the value of d in equation (iv):

`\to 3b+4 ((7)/(2))=8\\\\\to 3b+4 * (7)/(2)=8\\\\\to 3b+14=8\\\\\to 3b =8-14\\\\\to 3b = -6\\\\\to b= (-6)/(3)\\\\\to b= -2`

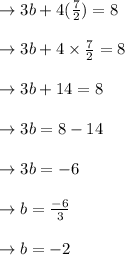
The final answer is "
`\bold{\left[\begin{array}{cc}a&b\\c&d\end{array}\right] = \left[\begin{array}{cc}7&-2\\ -(1)/(2)&(7)/(2)\end{array}\right]}`".