Question

Y=x^2-6x-16 in vertex form

Answer 1

`y=(x-3)^(2) -25`

Explanation:

The standard form of a quadratic equation is
`y=ax^(2) +bx+c`

The vertex form of a quadratic equation is
`y=a(x-h)^(2) +k`

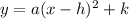
The vertex of a quadratic is (h,k) which is the maximum or minimum of a quadratic equation. To find the vertex of a quadratic, you can either graph the function and find the vertex, or you can find it algebraically.

To find the h-value of the vertex, you use the following equation:

`h=(-b)/(2a)`

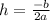
In this case, our quadratic equation is
`y=x^(2) -6x-16`. Our a-value is 1, our b-value is -6, and our c-value is -16. We will only be using the a and b values. To find the h-value, we will plug in these values into the equation shown below.

`h=(-b)/(2a)` ⇒
`h=(-(-6))/(2(1))=(6)/(2) =3`

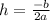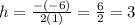
Now, that we found our h-value, we need to find our k-value. To find the k-value, you plug in the h-value we found into the given quadratic equation which in this case is
`y=x^(2) -6x-16`

`y=x^(2) -6x-16` ⇒
`y=(3)^(2) -6(3)-16` ⇒
`y=9-18-16` ⇒
`y=-25`

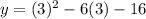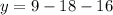This y-value that we just found is our k-value.

Next, we are going to set up our equation in vertex form. As a reminder, vertex form is:
`y=a(x-h)^(2) +k`

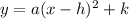
a: 1

h: 3

k: -25

`y=(x-3)^(2) -25`

Hope this helps!