Answer:
The roadrunner will take approximately 5.285 seconds to catch up to the rattlesnake.
Step-by-step explanation:
From the statement we notice that:
1) Rattlesnake moves a constant speed (
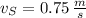 ), whereas the roadrunner accelerates uniformly from rest. (
), whereas the roadrunner accelerates uniformly from rest. (
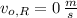 ,
,
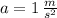 )
)
2) Initial distance between the roadrunner and rattlesnake is 10 meters. (
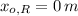 ,
,
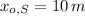 )
)
3) The roadrunner catches up to the snake at the end. (
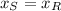 )
)
Now we construct kinematic expression for each animal:
Rattlesnake
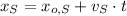
Where:
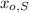 - Initial position of the rattlesnake, measured in meters.
- Initial position of the rattlesnake, measured in meters.
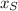 - Final position of the rattlesnake, measured in meters.
- Final position of the rattlesnake, measured in meters.
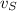 - Speed of the rattlesnake, measured in meters per second.
- Speed of the rattlesnake, measured in meters per second.
 - Time, measured in seconds.
- Time, measured in seconds.
Roadrunner
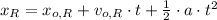
Where:
 - Initial position of the roadrunner, measured in meters.
- Initial position of the roadrunner, measured in meters.
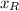 - Final position of the roadrunner, measured in meters.
- Final position of the roadrunner, measured in meters.
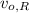 - Initial speed of the roadrunner, measured in meters per second.
- Initial speed of the roadrunner, measured in meters per second.
 - Acceleration of the roadrunner, measured in meters per square second.
- Acceleration of the roadrunner, measured in meters per square second.
 - Time, measured in seconds.
- Time, measured in seconds.
By eliminating the final positions of both creatures, we get the resulting quadratic function:

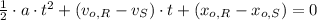
If we know that
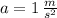 ,
,
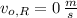 ,
,
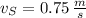 ,
,
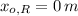 and
and
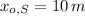 , the resulting expression is:
, the resulting expression is:
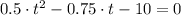
We can find its root via Quadratic Formula:
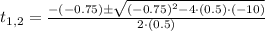
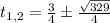
Roots are
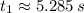 and
and
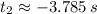 , respectively. Both are valid mathematically, but only the first one is valid physically. Hence, the roadrunner will take approximately 5.285 seconds to catch up to the rattlesnake.
, respectively. Both are valid mathematically, but only the first one is valid physically. Hence, the roadrunner will take approximately 5.285 seconds to catch up to the rattlesnake.