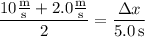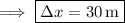Use the formula,
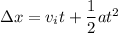
where
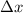 is the cart's displacement (from the origin),
is the cart's displacement (from the origin),
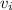 is its initial speed,
is its initial speed,
 is its acceleration, and
is its acceleration, and
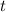 is time.
is time.
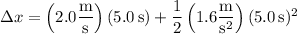
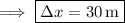
Alternatively, since acceleration is constant, we have
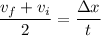
That is, we have these two equivalent expressions for average velocity, where
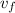 is the cart's final velocity. Solve for
is the cart's final velocity. Solve for
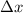 :
: