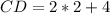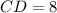Answer:
1.
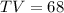
2.
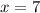
3.
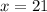
4.
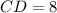
Explanation:
Solving (1):
Given


Required
Determine TV
To solve TV, we make use of the following formula;
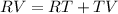
Substitute values for RT and RV
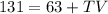
Make TV the subject of formula
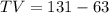
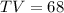
Solving (2):
Given


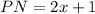
Required
FInd x
To solve x, we make use of the following formula;
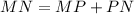
Substitute values for MP, MN and NP
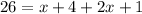
Collect Like Terms

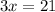
Divide both sides by 3
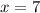
Solving (3):
Given
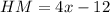
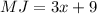
Required
Find x
Since M is the midpoint;
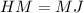
This gives
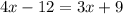
Collect Like Terms
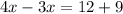
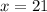
Solving (4):
Given
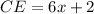
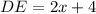
Required
FInd CD
Since D is the midpoint;

and

Substitute CD for DE
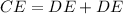
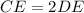
Substitute values for CE and DE
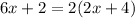
Open Bracket

Collect Like Terms
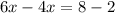
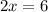
Divide both sides by 2
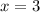
Recall that;

So;
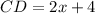
Substitute 2 for x