Question

2. Find the slope of a line that passes through (-2, -3) and (1, 1). (1 point)

Answer 1

Answer:4/3

Explanation:

Use the slope formula

m =
`(y2-y1)/(x2-x1)`

`(1-(-3))/(1-(-2)) = 4/3`

Answer 2

The slope of a line that passes through (-2, -3) and (1, 1) is 4/3.

Step-by-step explanation:

Here's the required formula to find slope line :

`\star{\underline{\boxed{\sf{m = (y_2 - y_1)/(x_2 - x_1)}}}}`

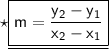
Here, we have provided :

`\begin{gathered} \footnotesize\rm {\underline{\underline{Where}}}\begin{cases}& \sf y_2 = 1\\& \sf y_1 = - 3\\ & \sf x_2 = 1\\ & \sf x_1 = - 2\end{cases} \end{gathered}`

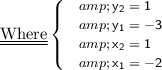
Substituting the values in the formula to find slope line :

`\begin{gathered} \qquad{\longrightarrow{\sf{m = (y_2 - y_1)/(x_2 - x_1)}}} \\ \\ \qquad{\longrightarrow{\sf{m = ((1) - ( - 3))/(1 - ( - 2))}}} \\ \\ \qquad{\longrightarrow{\sf{m = (1 + 3)/(1 + 2)}}} \\ \\ \qquad{\longrightarrow{\sf{m = (4)/(3)}}} \\ \\ \qquad{\star{\underline{\boxed{\frak{m = (4)/(3)}}}}} \end{gathered}`

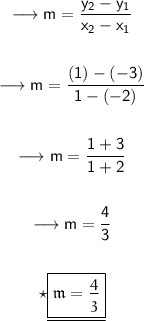
Hence, the slope line is 4/3.

`\rule{300}{2.5}`