|7 + 8x| > 5 I've tried solving this inequality multiple times and I just can't get it right. I don't know what I'm doing wrong. please help​

Question

`|7 + 8x| > 5`

I've tried solving this inequality multiple times and I just can't get it right. I don't know what I'm doing wrong. please help​

Answer 1

The absolute value is defined as

`|x|=\begin{cases}x&\text{if }x\ge0\\-x&\text{if }x<0\end{cases}`

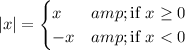
So for example, if x = 3, then |x| = |3| = 3, since 3 is positive. On the other hand, if x = -5, then |x| = |-5| = -(-5) = 5, since -5 is negative. The absolute value is always positive.

For the inequality |7 + 8x| > 5, you consider the two cases where the argument to the absolute value (the expression you find inside the bars) is either positive or negative.

• If 7 + 8x ≥ 0, then |7 + 8x| = 7 + 8x, so that

`|7+8x|>5\implies 7+8x>5 \implies 8x>-2 \implies x>-\frac14`

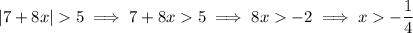
• Otherwise, if 7 + 8x < 0, then |7 + 8x| = -(7 + 8x), so that

`|7+8x|>5\implies-(7+8x)>5\implies7+8x<-5\implies8x<-12\implies x<-\frac32`

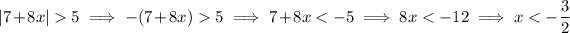
The solution to the inequality is the union of these two intervals.