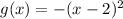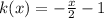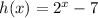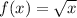Answer:
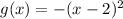
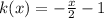
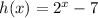
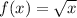
Explanation:
Given
Input = 6
Expected Output = 11
Process:
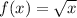
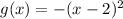
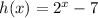
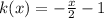
Required
Arrange the processes to give an output of 11
To answer this question, I'll make use of trial by error methods.
After some attempts, the following is the order of the processes;
Set x = 6
Substitute 6 for x in g(x)
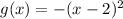
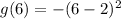
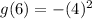
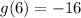
Substitute -16 for x in k(x)


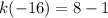
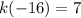
Substitute 7 for x in h(x)
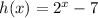

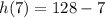
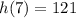
Substitute 121 for x in f(x)
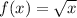
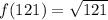
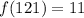
Hence, the processes is: