Answer:
c. 10 cm
Explanation:
The parallel sides of trapizium are the bases so
base 1(B1) =9cm , base(B2)= 12cm
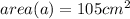
the perpendicular distance means the height so lets find the height
area of trapizium= B1 + B2 × h
2
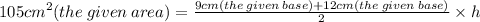
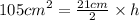
now we crisscross
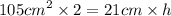
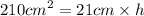
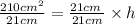
h = 10 cm
hope u like it ❤️❤️❤️
For any question comment me