Question

Its volume V. If r varies directly as s and inversly as t, r=27, when s=18 and t=2 find:

1. r when t=3 and s=27 2.
2. s when t=2 and r=3 3.
3. t when r=1 and s=6 4.
4. r when s=4 and 1=2 5.
5. s when t=5 and r=6​

Answer 1

===================================

`\large \sf \underline{Problem:}`

Its volume V. If r varies directly as s and inversly as t, r=27, when s=18 and t=2 find:

• 1.) r when t=3 and s=27
• 2.) s when t=2 and r=3
• 3.) t when r=1 and s=6
• 4.) r when s=4 and 1=2
• 5.) s when t=5 and r=6

===================================

`\large \sf \underline{Answers:}`

`\qquad \quad \huge \sf{1. r= 27} \\ \\ \qquad \huge \sf{2. s= 2 } \\ \\ \qquad \quad \huge \sf{3. t = 18} \\ \\ \qquad \huge \sf{4. r = 6 } \\ \\ \qquad \quad \huge \sf{5. s = 10}`

===================================

`\large \sf \underline{Solution:}`

Combined Variation:

`\large\bold{r=(ks)/(t)}\:\:,\:\:\sf s=(rt)/(k)\:\:,\:\:\sf t=(ks)/(r)\:\:,\:\:\sf k=(rt)/(s)`

Given:

• r = 27
• s = 18
• t = 2

Find the constant (k)

`\begin{gathered}\begin{aligned}&\sf k=(rt)/(s)\\&\sf k=(27(2))/(18)\\&\sf k=(54)/(18)\\&\sf k=3\end{aligned}\end{gathered}`

Use k = 3 to solve the following

Number 1:

`\begin{gathered}\begin{aligned}&\sf r=(ks)/(t)\\&\sf r=(\cancel3* 27)/(\cancel3)\\&\underline{\bold{\pmb{r=27}}}\end{aligned}\end{gathered}`

Number 2:

`\begin{gathered}\begin{aligned}&\sf s=(rt)/(k)\\&\sf s=(\cancel3* 2)/(\cancel3)\\&\underline{\bold{\pmb{s=2}}}\end{aligned}\end{gathered}`

Number 3:

`\begin{gathered}\begin{aligned}&\sf t=(ks)/(r)\\&\sf t=(3* 6)/(1)\\&\underline{\bold{\pmb{t=18}}}\end{aligned}\end{gathered}`

Number 4:

`\begin{gathered}\begin{aligned}&\sf r=(ks)/(t)\\&\sf r=(3* \cancel4)/(\cancel2)\\&\sf r=3* 2\\&\underline{\bold{\pmb{r=6}}}\end{aligned}\end{gathered}`

Number 5:

`\begin{gathered}\begin{aligned}&\sf s=(rt)/(k)\\&\sf s=(\cancel6 * 5)/(\cancel3)\\&\sf s=2* 5\\&\underline{\bold{\pmb{s=10}}}\end{aligned}\end{gathered}`

===================================

#LetEarthBreathe

Answer 2

`\qquad\qquad\huge\underline{{\sf Answer}}`

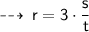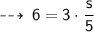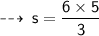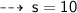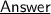
According to the question :

`\qquad \sf  \dashrightarrow \:r \propto s`

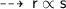
and

`\qquad \sf  \dashrightarrow \:r \propto (1)/(t)`

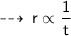
Now, by both equations we can infer that ~

`\qquad \sf  \dashrightarrow \:r \propto (s)/(t)`

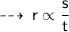
now, assume k to be a proportionality constant

`\qquad \sf  \dashrightarrow \:r = k \cdot (s)/(t)`

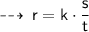
Now, plug in the value of given values, to find value of k ~

`\qquad \sf  \dashrightarrow \:27 = (18)/(2) \cdot k`

`\qquad \sf  \dashrightarrow \:27 = 9{} k`

`\qquad \sf  \dashrightarrow \:k = 27 / 9`

`\qquad \sf  \dashrightarrow \:k = 3`

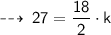
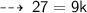
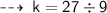
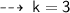
Now, let's evaluate the required values ~

# Question 1

`\qquad \sf  \dashrightarrow \:r = 3 \cdot (s)/(t)`

`\qquad \sf  \dashrightarrow \:r = 3 \cdot (27)/( 3)`

`\qquad \sf  \dashrightarrow \:r = 27`

# Question 2

`\qquad \sf  \dashrightarrow \:r= 3 \cdot (s)/(t)`

`\qquad \sf  \dashrightarrow \:3= 3 \cdot (s)/(2)`

`\qquad \sf  \dashrightarrow \:{s}{} = (3 * 2)/(3)`

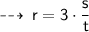
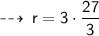
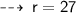
`\qquad \sf  \dashrightarrow \:s = 2`

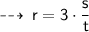
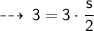
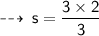
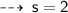
# Question 3

`\qquad \sf  \dashrightarrow \:r= 3 \cdot (s)/(t)`

`\qquad \sf  \dashrightarrow \:1= 3 \cdot (6)/(t)`

`\qquad \sf  \dashrightarrow \:t = 6\cdot3`

`\qquad \sf  \dashrightarrow \:t = 18`

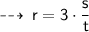
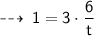
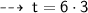
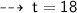
# Question 4

`\qquad \sf  \dashrightarrow \:r = 3 \cdot (s)/(t)`

`\qquad \sf  \dashrightarrow \:r = 3 \cdot (4)/(2)`

`\qquad \sf  \dashrightarrow \:r = (12)/(2)`

`\qquad \sf  \dashrightarrow \:r =6`

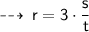
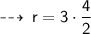
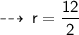
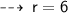
# Question 5

`\qquad \sf  \dashrightarrow \:r = 3 \cdot (s)/(t)`

`\qquad \sf  \dashrightarrow \:6= 3 \cdot (s)/(5)`

`\qquad \sf  \dashrightarrow \:s = (6 * 5)/(3)`

`\qquad \sf  \dashrightarrow \:s = 10`