Question

The product of two whole number is 462 and their sum is 43. What are the two numbers?

Answer 1

21 and 22

Explanation:

Let the two whole numbers be a and b.

Their product is 462. Hence, we can write that:

`ab=462`

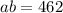
Likewise, because their sum is 42:

`a+b=43`

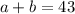
This yields a system of equations:

`\displaystyle \begin{cases} ab = 462 \\ a + b = 43 \end{cases}`

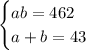
We can solve the system using substitution.

Isolating one variable in the second equation yields:

`a=43-b`

From substitution:

`(43-b)(b)=462`

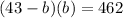
Distributing yields:

`-b^2+43b=462`

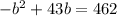
Solve for b by factoring:

`\displaystyle \begin{aligned} b^2 - 43d & = -462 \\ \\ b^2 - 43d + 462 & = 0 \\ \\ (b-21)(b-22) &= 0 \\ \\ b = 21 \text{ or } b & = 22 \end{aligned}`

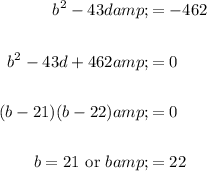
Solve for a:

`\displaystyle \begin{aligned} a& =43-(21) & \text{ or } a& =43-(22) \\ a&=22&\text{ or } a&=21\end{aligned}`

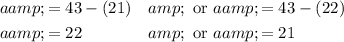
In conclusion, the two whole numbers are 21 and 22.