Question

Suppose now that you wanted to determine the density of a small crystal to confirm that it is phosphorus. From the literature, you know that phosphorus has a density of 1.82 . How would you prepare 20.0 mL of the liquid mixture having that density from pure samples of ( = 1.492 g/mL) and ( = 2.890 g/mL)? (Note: 1 mL = 1 .)

Answer 1

Volume of
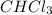`CHCl_3` = 15.31 mL

Volume of
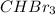`CHBr_3` = 4.69 mL

Step-by-step explanation:

Given that:

the density of the mixture = 1.82 g/mL

From the density of the pure samples

The density of
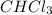`CHCl_3` = 1.492 g/mL

The density of
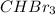`CHBr_3` = 2.890 g/mL

The total volume of the liquid mixture = 20.0 mL

Suppose the volume of
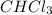`CHCl_3` = P ml

and the volume of
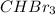`CHBr_3` = Q ml

the sum of their volumes should be equal to the total volume of the mixture

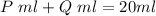`P \ ml + Q \ ml = 20 ml` ----- (1)

However, we know that Density = mass/volume

∴ mass = density × volume

The equation can now be expressed as:

`\mathtt{(Density \ of \ CHCl_3 * Vol. \ of \ CHCl_3 ) + (Density \ of \ CHBr_3 * \ volume \ of \ CHBr_3)} = \mathtt{ (Density \ of \ mixture * volume \ of \ the \ mixture)}`

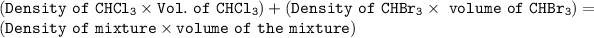
1.492 g/mL × P mL + 2.890 g/mL × Q mL = 1.82 g/mL × 20 mL ---- (2)

From equation (1) ;

let Q = 20 - P

The replace the value of P into equation (2)

1.492 g/mL × P mL + 2.890g/mL × (20 - P) mL = 1.82 g/mL × 20 mL

1.492 P g + 57.8g - 2.890 P g = 36.4g

1.492 P g - 2.890 P g = 36.4g - 57.8g

-1.398 P g = -21.4g

P = -21.4g/-1.398g

P = 15.31 mL

Q = 20 - P

Q = (20 - 15.31) mL

Q = 4.69 mL

∴

Volume of
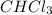`CHCl_3` = 15.31 mL

Volume of
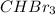`CHBr_3` = 4.69 mL