Question

Given directed line segment KM , find the coordinates of L such that the ratio

of KL to KM is 1:3. Plot point L. Round to the nearest tenth.
K

Answer 1

The answer is below

Step-by-step explanation:

The question is not complete, the coordinates of K and M are not given. Let us assume The coordinates are at K(1, -6) and M(9,-2)

Answer: If a line segment AB with coordinates at
`(x_1,y_1)\ and\ (x_2,y_2)` is divided by a point O(x, y) in the ratio n:m, the coordinates of point O is given by the formula:

`x=(n)/(n+m)(x_2-x_1)+x_1 \\\\y=(n)/(n+m)(y_2-y_1)+y_1`

K(1, -6) and M(9,-2) are divided in ratio 1:3 by point L. Let us assume L is at (x,y), hence the coordinate of point L is given as:

`x=(n)/(n+m)(x_2-x_1)+x_1=(1)/(1+3)(9-1)+1=(1)/(4)(8)+1=3 \\\\y=(n)/(n+m)(y_2-y_1)+y_1=(1)/(1+3)(-2-(-6))+(-6)=(1)/(4) (4)-6=-5`

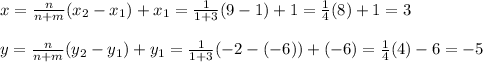
Point L is at (3, -5)