Answer:
Seven isn't part of the set of irrational numbers.
Explanation:
Seven and the Set of all Natural Numbers
Start with the smallest set among the choices. The set of all natural numbers,
 , starts with
, starts with
 (or
(or
 , for some people.) A number
, for some people.) A number
 is in
is in
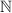 (write
(write
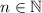 ) if and only if
) if and only if
 is in
is in
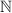 . Conversely, if
. Conversely, if
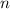 is indeed in
is indeed in
 , then
, then
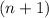 would also be in
would also be in
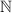 . For
. For
 :
:
 .
.
 .
.
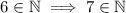 .
.
Therefore,
 is indeed in the set of all natural numbers.
is indeed in the set of all natural numbers.
Seven and the Set of all Integers
Similarly, a number
 is in the set of integers,
is in the set of integers,
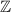 , if and only if either
, if and only if either
 or
or
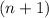 is (or both are) in
is (or both are) in
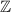 .
.
Conversely, if a number
 is in
is in
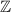 , then both
, then both
 and
and
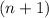 will be in
will be in
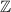 .
.
It can be shown in a similar iterative way that
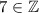 .
.
Alternatively, consider the fact that the set of all natural numbers,
 , is a subset of the set of all integers,
, is a subset of the set of all integers,
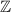 . Therefore,
. Therefore,
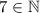 implies that
implies that
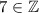 .
.
Seven and the Set of all Rational Numbers
A number
 is a member of the set of all rational numbers
is a member of the set of all rational numbers
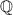 if and only if there exists two integers
if and only if there exists two integers
 and
and
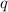 such that:
such that:
 .
.
 and
and
 are both integers. If
are both integers. If
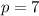 and
and
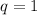 , then
, then
 . Hence,
. Hence,
Alternatively, note that the set of all integers,
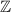 , is a subset of the set of all rational numbers,
, is a subset of the set of all rational numbers,
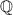 . Therefore, the fact that
. Therefore, the fact that
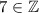 would imply that
would imply that
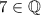 .
.
Seven and the Set of all Irrational Numbers
A number is in the set of all irrational numbers if and only if:
- this number is in the set of all real numbers, and
- this number is not in the set of all rational numbers. (Hence "irrational.")
Therefore, the fact that
 is a rational number implies that it is not an irrational number.
is a rational number implies that it is not an irrational number.