Question

1) El producto de dos números naturales consecutivos es 272. ¿Cuáles son esos números?

2) Hallar dos números naturales tales que su suma es 28 y la diferencia de sus cuadrados es 56.

3) Halla el lado de un cuadrado tal que la suma de su área más su perímetro es numéricamente igual a 252.

4) Se quiere vallar una finca rectangular que tiene de largo 25 m más que de ancho y cuya diagonal mide 125 m. ¿Cuántos metros de valla se necesitan?

5) La edad de un niño será dentro de tres años un cuadrado perfecto, y hace tres años que su edad era precisamente la raíz cuadrada de este cuadrado. ¿Qué edad tiene?

Answer 1

1) 135 y 137, 2) 13 y 15, 3) El lado del cuadrado es de 14 unidades, 4) Se necesita 350 metros de valla, 5) El niño tiene 6 años de edad.

Explanation:

1) El conjunto de los números naturales comprende al subconjunto de los números reales que son enteros y positivos. El enunciado se puede traducir con la siguiente expresión numérica:

`x + (x+n) = 272`

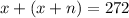
Donde
`x` y
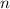`n` son números naturales. Se despeja
`x`:

i)
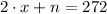`2\cdot x + n = 272` Propiedad asociativa/Definición de adición

ii)
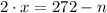`2\cdot x = 272-n` Compatibilidad con la adición/Existencia del inverso aditivo/Propiedad modulativa/Definición de sustracción

iii)
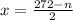`x = (272-n)/(2)` Compatibilidad con la multiplicación/Existencia del inverso multiplicativo/Propiedad modulativa/Definición de división

iv)
`x = (272)/(2)-(n)/(2)`
`(x+y)/(z) = (x)/(z) + (y)/(z)`

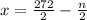
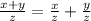
v)
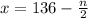`x = 136 - (n)/(2)` Definición de división/Resultado

Puesto que
`x` y
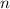`n` son números naturales,
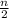`(n)/(2)` también debe ser entero y para garantizar la consecución entre los números,
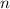`n` debe ser el elemento natural más pequeño posible. El número natural más pequeño es 1, por tanto, el valor mínimo de
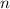`n` es 2. En consecuencia, el valor de
`x` es:

`x = 136-(2)/(2)`

`x = 136-1`

`x = 135`

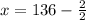
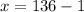
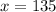
Los dos números naturales consecutivos son 135 y 137.

2) El enunciado se puede traducir en las siguientes dos ecuaciones matemáticas:

`x+y = 28`

`x^(2)-y^(2) = 56`

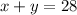
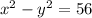
Se despeja una de las variables de la primera ecuación y se elimina la variable correspondiente en la segunda ecuación:

`x = 28-y`

`(28-y)^(2)-y^(2) = 56`

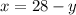
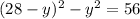
Se expande la ecuación resultante por álgebra de reales:

`784-56\cdot y +y^(2)-y^(2) = 56`

`784-56\cdot y = 56`

`56\cdot y = 784-56`

`56\cdot y = 728`

`y = 13`

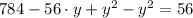
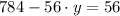
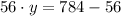
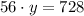
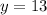
Finalmente, se halla el valor de la variable restante:

`x = 28-13`

`x = 15`

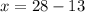
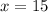
Los dos números naturales son 13 y 15.

3) Las fórmulas para el área (
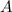`A`) y el perímetro del cuadrado (
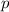`p`) son, respectivamente:

`A = l^(2)`

`p = 4\cdot l`

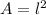
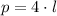
Donde
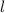`l` es la longitud del lado del cuadrado.

De acuerdo con el enunciado, existe la siguiente condición:

`A + p = 252`

`l^(2)+4\cdot l = 252`

`l^(2)+4\cdot l -252 = 0`

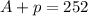
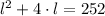
La ecuación resultante es un polinomio de segundo orden, cuyas raíces se obtienen por la Fórmula Cuadrática:

`l_(1) = 14` y
`l_(2) = -18`

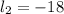
La primera raíz es la única solución razonable para la condición dada.

El lado del cuadrado es de 14 unidades.

4) Dado que la finca tiene una área rectangular y que se conoce la medida de la diagonal así como la diferencia entre el largo y el ancho, se puede determinar las variables restantes a partir del Teorema de Pitágoras:

`d^(2) = l^(2)+w^(2)`

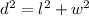
Donde:

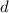`d` - Diagonal, medida en metros.

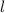`l` - Largo, medido en metros.

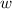`w` - Ancho, medido en metros.

Además, las relaciones son las siguientes:

`l = w + 25\,m`

`d = 125\,m`

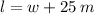
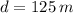
Se desarrolla y simplifica la identidad pitagórica hasta obtenerse un polinomio de segundo orden:

`125^(2) = (w+25)^(2)+w^(2)`

`2\cdot w^(2)+50\cdot w -15000 = 0`

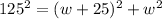
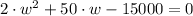
Las raíces del polinomio se hallan con ayuda de la Fórmula Cuadrática:

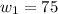`w_(1) = 75` y
`w_(2) = -100`

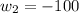
Solo la primera raíz ofrece una solución razonable, el ancho del rectángulo es de 75 metros. Por último, se halla el largo de la figura:

`l = 75\,m+25\,m`

`l = 100\,m`

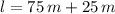
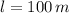
El largo del rectángulo es de 100 metros.

El perímetro del rectángulo (
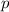`p`), medido en metros, es calculado por la siguiente fórmula:

`p = 2\cdot (w+l)`

`p = 2\cdot (75\,m+100\,m)`

`p = 350\,m`

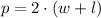
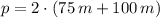
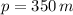
Se necesita 350 metros de valla.

5) Sea
`x` la edad actual del niño y
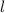`l` el lado del cuadrado. Entonces:

`x + 3 = l^(2)`

`x -3 = l`

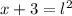
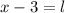
Se reemplaza el lado del cuadrado en la primera ecuación con ayuda de la segunda ecuación:

`x+3 = (x-3)^(2)`

`x +3 = x^(2)-6\cdot x + 9`

`x^(2)-7\cdot x+6 = 0`

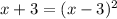
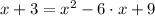
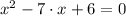
Las raíces se obtienen por factorización:

`(x-6)\cdot (x-1) = 0`

`x = 6 \,\wedge \,x = 1`

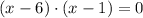
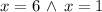
Ambas raíces son parecen razonables, se comprueba cada una para ver si satisfacen las condiciones del enunciado:

x = 1

`1+3 = l^(2)`

`4 = l^(2)`

`1-3 = l`

`-2 = l`

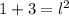
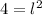
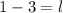
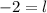
Si bien está matemáticamente bien, no lo es en lo que respecta a edad.

x = 6

`6+3 = l^(2)`

`9 = l^(2)`

`6-3 = l`

`3 = l`

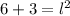
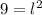
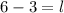
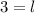
Esta solución es correcto en cuanto a matemática y edad.

El niño tiene 6 años de edad.