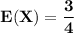Answer:
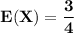
Explanation:
From the given data, the cumulative distribution function of a random variable can be represented as:

The objective is to estimate E(X), to do that, let's first evaluate the probability density function by differentiating the cumulative distribution function from above.
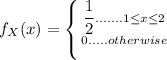
∴
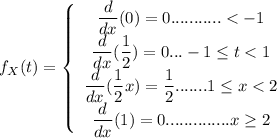
The expected value of x i
.e E(X) can now be estimated by taking the integral:

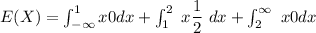
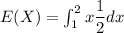
![E(X) = (1)/(2)[(x^2)/(2)]^2_1](https://img.qammunity.org/2021/formulas/mathematics/college/dtjjoro90w01vaena86rr6mf55la7ndb88.png)
![E(X) = (1)/(2)[(4)/(2)-(1)/(2)]](https://img.qammunity.org/2021/formulas/mathematics/college/ki32yofkkxdqo904nnan1lt74rmbt5z83c.png)
![E(X) = (1)/(2) * [(3)/(2)]](https://img.qammunity.org/2021/formulas/mathematics/college/qb0lv4t6nop7l44lib3affti8kil408hos.png)