Question

1. Describe two ways the numbers in each proportion are related.

a) 5:20 = 125:500 b) 10:1 = 120:12 c) 75:25 = 300: 100
d) 1:3 = 16:48
2. Multiply between ratios to determine each value of n.
a) 2:5 = 8:n b) 2:n = 6:9 c) n:5 = 12:20
d) 8:n = 4:15
Need
Read
the lo
3. Multiply within ratios to determine each value of z.
a) 4:8 = 3:2 b) 5:2 = 6:18 c) z: 14 = 10:20
d) 3:21 = z:56​

Answer 1

Each value has been identified below.

Explanation:

(1) We have to describe two ways the numbers in each proportion are related;

(a) 5 : 20 = 125 : 500

One way of describing that the given ratios are in proportion is;

Product of means = Product of extremes

20
`*` 125 = 5
`*` 500

2500 = 2500

This shows that the given proportion is related.

Another way of describing that the given ratios are in proportion is;

As 5 : 20 = 125 : 500

We will check that;
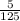`(5)/(125)` is equal to
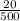`(20)/(500)` or not.

`(5)/(125) = (20)/(500)`

`(1)/(25) = (1)/(25)`

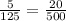
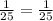
This shows that the given proportion is related.

(b) 10 : 1 = 120 : 12

One way of describing that the given ratios are in proportion is;

Product of means = Product of extremes

1
`*` 120 = 10
`*` 12

120 = 120

This shows that the given proportion is related.

Another way of describing that the given ratios are in proportion is;

As 10 : 1 = 120 : 12

We will check that;
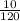`(10)/(120)` is equal to
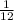`(1)/(12)` or not.

`(10)/(120) = (1)/(12)`

`(1)/(12) = (1)/(12)`

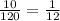
This shows that the given proportion is related.

(c) 75 : 25 = 300 : 100

One way of describing that the given ratios are in proportion is;

Product of means = Product of extremes

25
`*` 300 = 75
`*` 100

7500 = 7500

This shows that the given proportion is related.

Another way of describing that the given ratios are in proportion is;

As 75 : 25 = 300 : 100

We will check that;
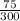`(75)/(300)` is equal to
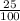`(25)/(100)` or not.

`(75)/(300) = (25)/(100)`

`(1)/(4) = (1)/(4)`

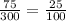
This shows that the given proportion is related.

(d) 1 : 3 = 16 : 48

One way of describing that the given ratios are in proportion is;

Product of means = Product of extremes

3
`*` 16 = 1
`*` 48

48 = 48

This shows that the given proportion is related.

Another way of describing that the given ratios are in proportion is;

As 1 : 3 = 16 : 48

We will check that;
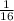`(1)/(16)` is equal to
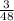`(3)/(48)` or not.

`(1)/(16) = (3)/(48)`

`(1)/(16) = (1)/(16)`

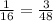
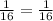
This shows that the given proportion is related.

(2) Now we have to determine each value of n in the following given ratios;

(a) 2 : 5 = 8 : n

As we know that Product of means = Product of extremes

5
`*` 8 = 2
`*` n

40 = 2n

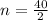`n=(40)/(2)` = 20

Hence, the value of n is 20.

(b) 2 : n = 6 : 9

As we know that Product of means = Product of extremes

n
`*` 6 = 2
`*` 9

6n = 18

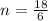`n=(18)/(6)` = 3

Hence, the value of n is 3.

(c) n : 5 = 12 : 20

As we know that Product of means = Product of extremes

5
`*` 12 = n
`*` 20

60 = 20n

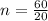`n=(60)/(20)` = 3

Hence, the value of n is 3.

(d) 8 : n = 4 : 15

As we know that Product of means = Product of extremes

n
`*` 4 = 8
`*` 15

4n = 120

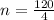`n=(120)/(4)` = 30

Hence, the value of n is 30.

(3) Now we have to determine each value of z in the following given ratios;

(a) 4 : 8 = 3 : z

As we know that Product of means = Product of extremes

8
`*` 3 = 4
`*` z

24 = 4z

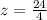`z=(24)/(4)` = 6

Hence, the value of z is 6.

(b) 5 : z = 6 : 18

As we know that Product of means = Product of extremes

z
`*` 6 = 5
`*` 18

6z = 90

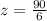`z=(90)/(6)` = 15

Hence, the value of z is 15.

(c) z : 14 = 10 : 20

As we know that Product of means = Product of extremes

14
`*` 10 = z
`*` 20

140 = 20z

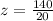`z=(140)/(20)` = 7

Hence, the value of z is 7.

(d) 3 : 21 = z : 56​

As we know that Product of means = Product of extremes

21
`*` z = 3
`*` 56

21z = 168

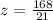`z=(168)/(21)` = 8

Hence, the value of z is 8.