Answer:
11) D. y=5/2x+5/2 , 12) B. y=8/5x+69/5, 14) A. y=-9/5x-67/5
Explanation:
11) The function of the perpendicular line can be found in terms of its slope and a given point by this formula:
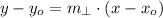
Where:
 ,
,
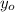 - Components of the given point, dimensionless.
- Components of the given point, dimensionless.
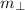 - Slope, dimensionless.
- Slope, dimensionless.
Besides, a slope that is perpendicular to original line can be calculated by this expression:

Where
 is the slope of the original line, dimensionless.
is the slope of the original line, dimensionless.
The original slope is determined from the explicitive form of the given line:
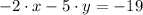
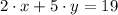
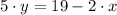
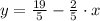
The original slope is
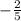 , and the slope of the perpendicular line is:
, and the slope of the perpendicular line is:
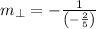
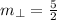
If
 ,
,
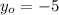 and
and
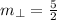 , then:
, then:
![y-(-5) = (5)/(2)\cdot [x-(-3)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/i1hkz0plv06y12ude4o5n1b0d6hg0nee3z.png)
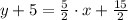
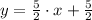
The right answer is D.
12) The function of the parallel line can be found in terms of its slope and a given point by this formula:
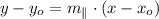
Where:
 ,
,
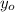 - Components of the given point, dimensionless.
- Components of the given point, dimensionless.
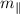 - Slope, dimensionless.
- Slope, dimensionless.
Its slope is the slope of the given, which must be transformed into its explicitive form:

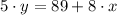
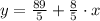
The slope of the parallel line is
 .
.
If
 ,
,
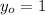 and
and
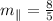 , then:
, then:
![y-1 = (8)/(5)\cdot [x-(-8)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/qlxnlp7mprm46th8zzy47radqz0v0gbh6n.png)
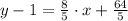
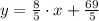
The correct answer is B.
14) The function of the perpendicular line can be found in terms of its slope and a given point by this formula:
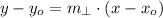
Where:
 ,
,
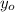 - Components of the given point, dimensionless.
- Components of the given point, dimensionless.
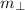 - Slope, dimensionless.
- Slope, dimensionless.
Besides, a slope that is perpendicular to original line can be calculated by this expression:

Where
 is the slope of the original line, dimensionless.
is the slope of the original line, dimensionless.
The original slope is determined from the explicitive form of the given line:
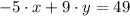
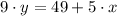
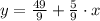
The original slope is
 , and the slope of the perpendicular line is:
, and the slope of the perpendicular line is:

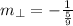
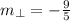
If
 ,
,
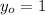 and
and
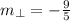 , then:
, then:
![y-1 = -(9)/(5)\cdot [x-(-8)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/1vvohbraepny56uhnsmr4rio99hgq2xqav.png)
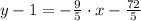
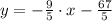
The correct answer is A.